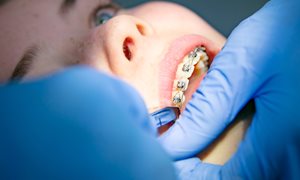
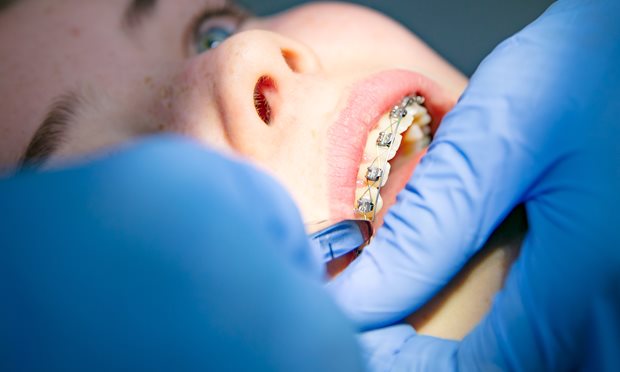
Over de afdeling Orthodontie
Beugels zijn tegenwoordig heel gewoon. Veel kinderen en volwassenen hebben er een. Met een beugel kunnen we scheve tanden rechtzetten. Ook kunnen we de groei van de kaken beïnvloeden.
De behandelingen vinden plaats op de polikliniek Orthodontie.
lees meerOver de afdeling Orthodontie
Beugels zijn tegenwoordig heel gewoon. Veel kinderen en volwassenen hebben er een. Met een beugel kunnen we scheve tanden rechtzetten. Ook kunnen we de groei van de kaken beïnvloeden. De behandelingen vinden plaats op de polikliniek Orthodontie.
Waarom gaat u naar de orthodontist?
- Als de groei van de boven- en onderkaak niet gelijk op gaat of is geweest;
- als tanden ver naar voren of scheef staan;
- als er te weinig of juist te veel ruimte in het gebit is;
- of als tanden en kiezen niet goed op elkaar passen en bijten daardoor bijvoorbeeld lastig is.
Sommige tandposities kunnen leiden tot schade aan het tandvlees, een scheefgroeiende onderkaak of een asymmetrie in het gezicht. Ook kunnen vooruitstekende tanden bij een val gemakkelijker beschadigen. Scheve tanden zijn moeilijker schoon te houden waardoor sneller tandvleesontstekingen ontstaan. De gezondheid staat dus voorop, een aantrekkelijke lach na de behandeling is een prettige bijkomstigheid.
Op welke leeftijd is een beugel mogelijk?
In principe is een orthodontische behandeling op elke leeftijd mogelijk. De conditie en het onderhoud van het gebit moeten wel goed zijn. Voor kinderen is de beste behandelperiode tussen de tien en vijftien jaar. We kunnen dan de kaakgroei nog beïnvloeden en we kunnen de ruimte gebruiken die vrijkomt tijdens het wisselen.
Bij volwassenen is tandverplaatsing even goed mogelijk als bij kinderen, als het gebit en de mond gezond zijn.
Samenwerken
We werken samen met de artsen van de afdeling Mond-, Kaak- en Aangezichtschirurgie en/of met gespecialiseerde tandartsen. Bijvoorbeeld wanneer niet alleen het gebit gereguleerd moet worden, maar ook de kaakstand gecorrigeerd. Of wanneer de orthodontische behandeling onderdeel is van een restauratieve behandeling.
Ook werken we samen met Expertisecentrum Schisis en Expertisecentrum Aangeboren tandafwijkingen voor de orthodontische behandeling van respectievelijk patiënten met schisis en craniofaciale afwijkingen, en patiënten met aangeboren tandafwijkingen.
Dit vindt allemaal plaats op het kliniekenplein van Tandheelkunde, in het nieuwe Centrum voor Mond & Gelaat.
Afspraakcheck
Kijk bij de digitale afspraakbalie na wanneer u een afspraak bij ons heeft.
naar afspraakcheckContact
Orthodontie is telefonisch bereikbaar via (024) 361 40 27.
Aanmelden bij orthodontie
Aanmelden kan via een online formulier. Let op: de wachttijd is momenteel ongeveer 4 maanden.
Wil je je aanmelden als patiënt? Gebruik het Aanmeldformulier voor patiënten.
Voor verwijzers
Gebruik het Aanmeldformulier voor verwijzers om je patiënt door te verwijzen.
In behandeling bij orthodontie
Hoe ziet het traject eruit?
De route naar een mooi en goed functionerend gebit in een harmonieus gelaat begint hier.
lees meerHoe ziet het traject eruit?
De route naar een mooi en goed functionerend gebit in een harmonieus gelaat begint hier. Hoe ziet een traject bij orthodontie eruit?
Eerste bezoek (eerste consult)
U gaat in gesprek met een orthodontist. Hij of zij kijkt of een behandeling nodig en zinvol is. Welke behandeling past, welke risico’s er zijn en welke kosten u kunt verwachten. Indien wenselijk kan soms direct overgegaan worden tot het verzamelen van de benodigde gegevens voor het opstellen van een behandelplan.
Ook kan het zijn dat eerst nog meegekeken moet worden door andere specialisten omdat medebehandeling door andere disciplines nodig is. U krijgt dan een vervolgafspraak voor een multidisciplinair spreekuur met bijvoorbeeld een Kaakchirurg of een tandarts voor Bijzondere Tandheelkunde
Soms zijn kinderen nog niet toe aan een orthodontische behandeling. Bijvoorbeeld wanneer er nog veel tanden gewisseld moeten worden of de kaak nog verder moet groeien. In dat geval volgt een herhalingsconsult na bijvoorbeeld een half of een heel jaar. Daarvoor sturen wij u dan t.z.t een nieuwe afspraakdatum.
Tweede bezoek
Mocht er een behandelwens bestaan en zijn er tijdens het eerste bezoek geen gegevens verzameld, dan verzamelen we tijdens dit tweede bezoek mond- en profielfoto’s, röntgenfoto’s en digitale gebitsmodellen. Met deze informatie beraden we ons op de aanpak van de behandeling.
Derde bezoek
Uw behandelaar legt de voorgestelde behandeling aan u uit naar aanleiding van de informatie die verzameld is tijdens het eerste of tweede bezoek. Hij of zij legt uit wat er gaat gebeuren:
- Wat is er precies aan de hand, en hoe lossen we het op:
- Welke behandeling of beugel is voor u het beste?
- Hoe lang gaat de behandeling ongeveer duren?
- Is er wellicht voorafgaand aan de behandeling nog voorbereiding nodig, bijvoorbeeld het verwijderen van kiezen of vullen van gaatjes door de tandarts?
U krijgt informatie over risico's, beperkingen en ongemakken.
Controlebezoeken
In de regel komt u tijdens de behandeling elke maand op controle. De gemiddelde duur van een behandeling is ongeveer 2-3 jaar. Zijn er tussentijds klachten, breekt er apparatuur of gaat er apparatuur op andere wijze kapot, dan vragen we direct contact met ons op te nemen.Er bestaan heel veel verschillende beugels. In de orthodontische praktijk noemen ze dat apparatuur. Er zijn binnen- en buitenbeugels en bij de binnenbeugels wordt er weer een onderscheid gemaakt tussen uitneembare en vastzittende beugels.
Medische gegevens
Voor ieders veiligheid vragen we u om ons steeds te informeren over medische bijzonderheden. Denk aan zwangerschap, medicijngebruik, ziektes, infecties etc. Bij gebruik van medicijnen zijn wij verplicht het medicatie overzicht bij uw gegevens te voegen. Dit overzicht vraagt u (kosteloos) op bij uw apotheek.
Behandelingen en apparatuur
De behandeling hangt af van de afwijking en de apparatuur die nodig is om het probleem te verhelpen.
lees meerBehandelingen en apparatuur
Hoe de behandeling er voor u uitziet, hangt af van de geconstateerde afwijking en de beugelapparatuur die nodig is om het probleem te verhelpen. We leggen graag uit welke behandelingen mogelijk zijn en welke apparatuur (voornamelijk beugels) gebruikt wordt. We onderscheiden daarbij de actieve behandeling en de retentiefase: waarin de nieuwe positie van de tanden en kiezen vastgehouden wordt.
Actieve behandeling
Er bestaan heel veel verschillende beugels. In de orthodontische praktijk noemen ze dat apparatuur. Er zijn binnen- en buitenbeugels en bij de binnenbeugels wordt er weer een onderscheid gemaakt tussen uitneembare en vastzittende beugels.
Tijdens een orthodontische behandeling is het regelmatig nodig verschillende soorten beugels gelijktijdig of direct na elkaar te gebruiken. De keuze voor de beugel die moet worden gebruikt hangt vooral af van het doel dat ermee bereikt moet worden. Met een auto kun je niet vliegen en een vliegtuig is niet geschikt om de weg op te gaan: je reisdoel moet bepalen welk vervoermiddel het meest geschikt is.
Behandelingen
- Stand boven- en onderkaak ten opzichte van elkaar corrigeren
Hier lees je meer over:- Activator
- Headgear (buitenboordbeugel)
- Herbst-beugel
- Boventandboog of bovenkaak verbreden
Hier lees je meer over:- Quad helix
- Verbreding van de bovenkaak
- MARPE-expansie van de bovenkaak
- Tandstand corrigeren
Hier lees je meer over:- Vaste of blokjesbeugel
- Clear aligners
- Uitneembare plaatbeugel
Nieuwe positie van de tanden en kiezen vasthouden
Na de actieve behandeling is het belangrijk om uw tanden en kiezen in de nieuwe positie vast te houden. Het weefsel en de tanden moeten zich aanpassen. Dit noemen we retentie.
Meestal gebeurt dat met een draadje achter de tanden (spalk) om te voorkomen dat de voortanden weer scheef gaan staan. Het spalkje blijft levenslang zitten. Komt het los, neem dan contact op om het te herstellen. Vaak wordt naast de geplaatste spalken ook een uitneembare beugel (retentieplaat) geplaatst, om zo de tanden en kiezen zo goed mogelijk in de nieuwe stand te houden.
Belangrijk! Als de spalk losraakt of de retentieapparatuur wordt niet naar behoren gedragen, dan bestaat het risico dat de tanden weer scheef gaan staan.
Lees meer over beugels om het resultaat van de behandeling vast te houden (retentie): de retentieplaat, de Essix retainer en retentiespalken.
Apparatuur en hulpmiddelen
We gebruiken verschillende beugels en hulpmiddelen bij onze behandelingen. Je leest op beugelapparatuur en hulpmiddelen voor de verschillende behandelingen meer over:
- Separeren
- Palatal bar
- Opbeetplaat
- Lipbumper
- Elastieken
- Intermaxillaire correctieveren
- Botankers en minischroefjes

Naar uw afspraak
Orthodontie bij het Radboudumc vindt plaats in het Tandheelkundegebouw.
Ingang: Tandheelkunde
Naar uw afspraak
Bezoekadres
Philips van Leydenlaan 25
6525EX Nijmegen
Routebeschrijving


Een probleem met je beugel wat nu?
Voor problemen met de beugel kun je (op afspraak) tussentijds langskomen. Kijk hier eerst voor tips over wat je zelf kunt doen.
lees meerEen probleem met je beugel wat nu?
Als er iets kapot is aan je beugel, kun je ons bellen om tussendoor extra langs te komen. Kom niet zomaar met een los slotje op controle! Buiten openingstijden kun je het antwoordapparaat beluisteren voor hulp. Het spoednummer is alleen bedoeld voor ernstige klachten die niet kunnen wachten tot na het weekend.
Hieronder staan verschillende tips om problemen met je beugel zelf op te lossen.
Tips
Een metaaldraad van de losse beugel is kapot
Beugel uitlaten en bellen voor een afspraak. Meestal kan de beugel gerepareerd worden.
De losse beugel drukt op het tandvlees
Beugel uitlaten en bellen voor een afspraak. Er moet iets van de beugel worden afgeslepen.
Er prikt een draad van de vaste beugel in de wang
Doe er een bolletje was op en bel voor een afspraak. Als het weekend of vakantie is, kan de dienstdoende orthodontist je helpen. Het draadje moet worden afgeknipt. U mag dit ook zelf proberen met een klein knippertje / schaartje.
Er is een bracket los.
Als het niet erg stoort, kan je het laten zitten en ons bellen voor overleg. Als het wel stoort, doe er dan een bolletje was op en bel voor een afspraak.
Er is een (ketting)elastiek losgeschoten
Knip alles wat stoort of los is eraf en bel voor een afspraak.
Er is een band om een kies los
Als je een (buiten)beugel eraan vast moet maken: de buitenbeugel niet meer dragen. Doe er eventueel een beetje was op en bel voor een afspraak.
Praktisch
-
Er is een stafpraktijk en een AIOS-praktijk.
lees meer
Praktijken binnen de polikliniek
De stafpraktijk
In de stafpraktijk wordt u door een staflid-orthodontist behandeld, samen met orthodontisch assistentes. Voor de stafpraktijk nemen wij op dit moment geen nieuwe patiënten meer aan.
De stafleden ontvangen u ook tijdens de spreekuren en voor bijvoorbeeld second opinions. Zij behandelen ook de patienten met schisis en andere craniofaciale aandoeningen.
De AIOS-praktijk
In de AIOS-praktijk wordt u behandeld door tandartsen in opleiding tot orthodontist. Dit gebeurt onder begeleiding van een ervaren staflid-orthodontist.
-
Bij de polikliniek gelden de tarieven die de NZA bepaald heeft.
lees meer
Kosten
Bij de polikliniek Orthodontie gelden de tarieven die de NZA bepaald heeft.
Er is wel verschil tussen behandeling bij de stafpraktijk en behandeling bij de praktijk van specialisten in opleiding (AIOS).
Opleidingskorting
Bij de stafpraktijk betaalt u voor wat er nodig is voor uw behandeling, zonder een maximum-limiet. Als u behandeld wordt in de onderwijspraktijk krijg u een opleidingskorting. Dat betekent dat er vanaf de start van de actieve behandeling maximaal € 2.750,00 gedeclareerd wordt voor de hele orthodontische behandeling.
Uitgezonderd zijn:
- De kosten voor bijkomende chirurgische of andere algemeen tandheelkundige verrichtingen;
- De techniek- en/of materiaalkosten voor behandeling met clear aligners, linguale apparatuur en palatinale botverankering;
- De kosten voor niet-nagekomen of te laat afgemelde afspraken;
- De kosten voor reparatie of vervanging van apparatuur door onzorgvuldig gebruik.
Als de tarieven wettelijk verhoogd worden kan het maximale bedrag worden aangepast. Aan het begin van uw behandeling bespreken we het maximumtarief dat op dat moment geldt.
Facturen
Rekeningen gaan meestal direct naar uw verzekeraar. Afspraken in uw verzekeringspolis bepalen of u geen factuur thuisgestuurd krijgt, of een deel ervan, of helemaal.
De rekeningen worden verzorgd door Netpoint Factoring (04 16 – 54 15 09). Van toepassing zijn de betalingsvoorwaarden van Netpoint Factoring B.V. (https://www.uwdeclaraties.nl/index.php).
Verzekeringen
Elke verzekeraar heeft diverse aanvullende pakketten waarin orthodontie is opgenomen. Voor een overzicht kunt u kijken op www.orthodontist.nl of www.vergelijkmondzorg.nl/orthodontie/
-
In april 2021 is de vakgroep weer gecertificeerd en voldoen we aan de laatste kwaliteitsnormen van de Nederlandse Vereniging van Orthodontisten.
-
Ondanks behandeling volgens de huidige stand van de wetenschap bestaat er een (kleine) kans op bijwerkingen.
lees meer
Risico's
Een orthodontische behandeling wordt volgens de huidige stand van de wetenschap uitgevoerd. Ook dan bestaat er een (kleine) kans op tijdelijke of blijvende bijwerkingen. Ook zijn er risico's.
Hier leest u meer over in de pdf:
Orthodontische behandeling - Informatie over risico's, beperkingen en ongemakken
Orthodontic treatment - Information about risks, side effects, limitations and discomfort -
Bij sommige sporten is gebitsbescherming nodig. Hoe werkt dat met een beugel?
lees meer
Gebitsbescherming
Bij sommige sporten is gebitsbescherming noodzakelijk of erg aan te raden. Bij uitneembare beugels is dat geen probleem. Bij de vaste beugel is een aanpasbare beschermer het handigst. Deze moet af en toe aangepast worden omdat de tanden natuurlijk steeds van plaats veranderen.
Na het afronden van de orthodontische behandeling is een op maat gemaakte gebitsbeschermer het beste en het prettigste.
Meer informatie
Radboudumc Expertisecentrum Schisis
U kunt bij ons Schisisteam terecht als uw kind geboren is met een spleet van de lip of van de kaak en het gehemelte.
lees meer
